Действующий
9.4.6 В случаях, когда фактическое значение условной гибкости стенки  превышает предельное значение
превышает предельное значение 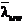 , вычисленное для сечений типа 1 по формулам таблицы 22, а для сечений типов 2 и 3 с учётом примечания 2 таблицы 22 (при
, вычисленное для сечений типа 1 по формулам таблицы 22, а для сечений типов 2 и 3 с учётом примечания 2 таблицы 22 (при  ), проверку устойчивости стержня по формулам (109), (115) и (116), а также при
), проверку устойчивости стержня по формулам (109), (115) и (116), а также при  по формуле (111), следует выполнять с учётом расчётной уменьшенной площади
по формуле (111), следует выполнять с учётом расчётной уменьшенной площади 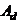 в соответствии с 7.3.6.
в соответствии с 7.3.6.
9.4.7 Устойчивость поясов (полок) внецентренно сжатых (сжато-изгибаемых) стержней с гибкостью  следует считать обеспеченной, если условная гибкость свеса пояса (полки)
следует считать обеспеченной, если условная гибкость свеса пояса (полки)  или поясного листа
или поясного листа  не превышает значений предельной условной гибкости
не превышает значений предельной условной гибкости 
 , определяемых по формулам в таблице 23.
, определяемых по формулам в таблице 23.
Тип сечения | Схема сечения и эксцентриситет | Условие применения формул | Предельная условная гибкость свеса пояса | ||||
1 |
| ||||||
2 |
| ||||||
3 |
| - | |||||
4 |
| ||||||
| Обозначение, принятое в таблице 23: | |||||||
9.4.8 Для полок (стенок) с отгибами (см. рисунок 5), значения предельной условной гибкости 
 , определяемые по формулам таблицы 23, следует умножать на коэффициент 1,5.
, определяемые по формулам таблицы 23, следует умножать на коэффициент 1,5.
9.4.9 При назначении сечений внецентренно сжатых и сжато-изгибаемых элементов по предельной гибкости (раздел 10.4) значения предельных условных гибкостей стенки  , определяемых по формулам таблицы 22, а также поясов
, определяемых по формулам таблицы 22, а также поясов 
 , определяемых по формулам таблицы 23 и согласно 9.4.8, следует увеличивать умножением на коэффициент
, определяемых по формулам таблицы 23 и согласно 9.4.8, следует увеличивать умножением на коэффициент  (здесь
(здесь  - меньшее из значений
- меньшее из значений  ,
,  ,
,  , использованное при проверке устойчивости элемента), но не более чем в 1,25 раза.
, использованное при проверке устойчивости элемента), но не более чем в 1,25 раза.
10.1.1 Расчетные длины сжатых элементов плоских ферм и связей в их плоскости  и из плоскости
и из плоскости  (рисунок 13, а), б), в), г), за исключением элементов, указанных в 10.1.2 и 10.1.3, следует принимать по таблице 24.
(рисунок 13, а), б), в), г), за исключением элементов, указанных в 10.1.2 и 10.1.3, следует принимать по таблице 24.
10.1.2 Расчётные длины  и
и  верхнего пояса фермы (неразрезного стержня) постоянного сечения с различными сжимающими или растягивающими усилиями на участках (число участков равной длины
верхнего пояса фермы (неразрезного стержня) постоянного сечения с различными сжимающими или растягивающими усилиями на участках (число участков равной длины  ) в предположении шарнирного сопряжения (рисунок 14, а) элементов решетки и связей, следует определять по формулам:
) в предположении шарнирного сопряжения (рисунок 14, а) элементов решетки и связей, следует определять по формулам:
где  - отношение усилия, соседнего с максимальным, к максимальному усилию в панелях фермы; при этом
- отношение усилия, соседнего с максимальным, к максимальному усилию в панелях фермы; при этом  ;
;
где  - отношение суммы усилий на всех участках (рассматриваемой длины между точками закрепления пояса из плоскости), кроме максимального, к максимальному усилию; при этом
- отношение суммы усилий на всех участках (рассматриваемой длины между точками закрепления пояса из плоскости), кроме максимального, к максимальному усилию; при этом  . При вычислении параметра
. При вычислении параметра 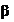 в формуле (137) растягивающие усилия в стержнях необходимо принимать со знаком "минус".
в формуле (137) растягивающие усилия в стержнях необходимо принимать со знаком "минус".
Направление продольного изгиба элемента фермы | Расчетные длины | ||
поясов | опорных раскосов и опорных стоек | прочих элементов решетки | |
| 1 В плоскости фермы | |||
| а) для ферм, кроме указанных в позиции 1,б | l | l | 0,8l |
| б) для ферм из одиночных уголков и ферм с прикреплением элементов решетки к поясам впритык | l | l | 0,9l |
| 2 В направлении, перпендикулярном к плоскости фермы | |||
| (из плоскости фермы) | |||
| а) для ферм, кроме указанных в позиции 2,б | |||
| б) для ферм с прикреплением элементов решётки к поясам впритык | |||
| 3 В любом направлении | 0,85l | l | 0,85l |
| Обозначения, принятые в таблице 24 (см. рисунок 13):l - геометрическая длина элемента (расстояние между центрами ближайших узлов) в плоскости фермы; | |||
Расчётные длины  и
и  ветви сквозной колонны постоянного сечения (неразрезного стержня) с различными сжимающими усилиями на участках (число участков равной длины
ветви сквозной колонны постоянного сечения (неразрезного стержня) с различными сжимающими усилиями на участках (число участков равной длины 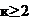 ) с граничными условиями, когда один конец стержня (нижний) жестко закреплен, а другой - шарнирно оперт в плоскости решетки при шарнирном креплении к нему элементов решетки (рисунок 14, б), следует определять по формулам:
) с граничными условиями, когда один конец стержня (нижний) жестко закреплен, а другой - шарнирно оперт в плоскости решетки при шарнирном креплении к нему элементов решетки (рисунок 14, б), следует определять по формулам:
где  - отношение усилия, соседнего с максимальным, к максимальному усилию в месте заделки; при этом
- отношение усилия, соседнего с максимальным, к максимальному усилию в месте заделки; при этом  ;
;
где  - отношение суммы усилий на всех участках, кроме максимального, к максимальному усилию в месте заделки; при этом
- отношение суммы усилий на всех участках, кроме максимального, к максимальному усилию в месте заделки; при этом  .
.
В обоих случаях l - длина участка (см. рисунки 13 и 14);  - расстояние между точками связей из плоскости стержня (см. рисунок 14), и расчёт на устойчивость следует выполнять на максимальное усилие.
- расстояние между точками связей из плоскости стержня (см. рисунок 14), и расчёт на устойчивость следует выполнять на максимальное усилие.
10.1.3 Расчётные длины  (когда они не зависят от соотношения усилий) элементов перекрёстной решётки, скрепленных между собой (см. рисунок 13, д), следует принимать по таблице 25. Определять расчетные длины пересекающихся связей (см. вид 1-1 рисунка 14, а) следует в соответствии с правилами по проектированию стальных конструкций.
(когда они не зависят от соотношения усилий) элементов перекрёстной решётки, скрепленных между собой (см. рисунок 13, д), следует принимать по таблице 25. Определять расчетные длины пересекающихся связей (см. вид 1-1 рисунка 14, а) следует в соответствии с правилами по проектированию стальных конструкций.
Конструкция узла пересечения элементов решётки | Расчетная длина | ||
растянутом | неработающем | сжатом | |
| Оба элемента не прерываются | / | ||
| Поддерживающий элемент прерывается и перекрывается фасонкой: | |||
| рассматриваемый элемент не прерывается | |||
| рассматриваемый элемент прерывается и перекрывается фасонкой | - | - | |
| Обозначения, принятые в таблице 25 (см. рисунок 13, д):l - расстояние от центра узла фермы (связи) до точки пересечения элементов; | |||
10.1.4 Радиусы инерции i сечений элементов из одиночных уголков при определении гибкости следует принимать:
при расчётной длине элемента не менее 0,85 l (где l - расстояние между центрами ближайших узлов) - минимальными  ;
;
в остальных случаях - относительно оси уголка, перпендикулярной или параллельной плоскости фермы ( или
или 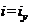 ), в зависимости от направления продольного изгиба.
), в зависимости от направления продольного изгиба.
10.2.1 Расчётные длины 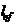 элементов структурных конструкций следует принимать по таблице 26 (l - геометрическая длина элемента - расстояние между центрами узлов структурных конструкций).
элементов структурных конструкций следует принимать по таблице 26 (l - геометрическая длина элемента - расстояние между центрами узлов структурных конструкций).
Элементы структурных конструкций | Расчётная длина | |
1 | Кроме указанных в позициях 2 и 3 | l |
2 | Неразрезные (не прерывающиеся в узлах) пояса, а также элементы поясов и решёток, прикрепляемых в узлах сваркой впритык к шаровым или цилиндрическим узловым элементам | 0,85l |
3 | Из одиночных уголков, прикрепляемых в узлах одной полкой: | |
| а) сварными швами или болтами (не менее двух), расположенными вдоль элемента, при | ||
| до 90 | l | |
| св. 90 до 120 | 0,90l | |
| св. 120 до 150 (только для элементов решётки) | 0,75l | |
| св. 150 до 200 (только для элементов решётки) | 0,70l | |
| б) одним болтом при | ||
| до 90 | l | |
| св. 90 до 120 | 0,95l | |
| св. 120 до 150 (только для элементов решётки) | 0,85l | |
| св. 150 до 200 (только для элементов решётки) | 0,80l | |
10.2.2 Радиусы инерции сечений i элементов структурных конструкций при определении гибкости следует принимать:
для сжато-изгибаемых элементов - относительно оси, перпендикулярной к или параллельной плоскости изгиба ( или
или  ); в остальных случаях - минимальными
); в остальных случаях - минимальными  .
.
10.2.3 Расчётные длины  и радиусы инерции сечений i сжатых, растянутых и ненагруженных элементов пространственных конструкций (рисунок 15) из одиночных уголков при определении гибкости следует принимать по таблицам 27, 28 и 29.
и радиусы инерции сечений i сжатых, растянутых и ненагруженных элементов пространственных конструкций (рисунок 15) из одиночных уголков при определении гибкости следует принимать по таблицам 27, 28 и 29.
10.2.4 Для определения расчетных длин раскосов по рисунку 15, в, при прикреплении их без фасонок к распорке и поясу сварными швами или болтами (не менее двух), расположенными вдоль раскоса, значение коэффициента расчетной длины 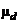 следует принимать по таблице 29 при значении n "До 2". В случае прикрепления их концов одним болтом значение
следует принимать по таблице 29 при значении n "До 2". В случае прикрепления их концов одним болтом значение  следует принимать по таблице 29 для прикрепления "Одним болтом без фасонки", а при вычислении значения
следует принимать по таблице 29 для прикрепления "Одним болтом без фасонки", а при вычислении значения 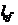 по таблице 27 вместо
по таблице 27 вместо  следует принимать
следует принимать  .
.
10.2.5 Расчётные длины  и радиусы инерции i элементов из труб или парных уголков следует принимать согласно 10.1.1 - 10.1.3.
и радиусы инерции i элементов из труб или парных уголков следует принимать согласно 10.1.1 - 10.1.3.
Элементы пространственных конструкций | Сжатые и непогруженные элементы | Растянутые элементы | ||
i | / | |||
| Пояса: | ||||
| по рисунку 15, а), б), в) | ||||
| по рисунку 15, г), д) | ||||
| по рисунку 15, е) | ||||
| Раскосы: | ||||
| по рисунку 15, а), д) | ||||
| по рисунку 15, б), в), г), е) | ||||
| Распорки: | ||||
| по рисунку 15, б), е) | - | - | ||
| по рисунку 15, в) | ||||
| Обозначения, принятые в таблице 27 (рисунок 15): | ||||
Конструкция узла пересечения элементов решетки | Условная длина раскоса | ||
растянутом | неработающем | сжатом | |
| Оба стержня не прерываются | |||
| Поддерживающий элемент прерывается и перекрывается фасонкой; рассматриваемый элемент не прерывается: | |||
| в конструкциях по рисунку 15, а) | |||
| в конструкциях по рисунку 15, д) | |||
| Узел пересечения элементов закреплен от смещения из плоскости грани (диафрагмой и т.п.) | |||
| Обозначение, принятое в таблице 28 (рисунок 15): | |||