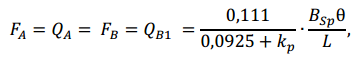Действующий
7.3.2.1 Напряжения в сечениях панелей и прогибы сплошных многослойных панелей с толстыми обшивками можно определить аналитически для часто встречающихся простых случаев.
7.3.2.2 Эпюры внутренних сил от воздействия внешней равномерно распределенной нагрузки и разности температур на обшивках в двухпролетных панелях приведены на рисунке 7.
а – усилия в панели от постоянной нагрузки; б – усилия в панели от разности температур на обшивках; 1, 2 – пролеты
7.3.2.3 Изгибающие моменты и поперечные силы в сечениях двухпролетной неразрезной панели, в пролетах и на опорах А (крайняя) и В (промежуточная) от равномерно распределенной нагрузки вычисляют по формулам:
MS1 − изгибающий момент в пролете панели с профилированной обшивкой; MSB− изгибающий момент на опоре панели с профилированной обшивкой;
BF1p − жесткость профилированной обшивки на единицу ширины панели; и FA и FB− опорные реакции на опорах А и В.
7.3.2.4 Изгибающие моменты и поперечные силы в сечениях двухпролетной неразрезной панели, в пролетах и на опорах А (крайняя) и В (промежуточная) от разности температур на обшивках панели вычисляют по формулам:
7.3.2.5 Эпюры внутренних сил от воздействия равномерно распределенной нагрузки и разности температур на обшивках в трехпролетных панелях приведены на рисунке 8. Изгибающие моменты и поперечные силы в сечениях трехпролетной неразрезной панели, в пролетах и на опорах А (крайняя) и В (промежуточная) от равномерно распределенной нагрузки определяются по формулам:
а – усилия в панели от постоянной нагрузки; б – усилия в панели от разности температур на обшивках; 1, 2, 3 – пролеты
Рисунок 8 – Эпюры M и Q в трехслойных панелях и их обшивках от поперечной равномерно распределенной нагрузки и разности температур на обшивках панели
7.3.2.6 Изгибающие моменты и поперечные силы в сечениях трехпролетной неразрезной панели, в пролетах и на опорах А (крайняя) и В (промежуточная) от разности температур вычисляют по формулам:
8.1.1 Сжатая плоская поверхность обшивки панели в предельном состоянии может потерять устойчивость из плоскости панели (образуются складки); подобное может произойти как в пролете, так и над опорами. Максимальное напряжение от изгибающего момента Mu, которое может выдержать обшивка, может быть вычислено по формуле
8.1.2 Критические напряжения потери местной устойчивости плоской обшивки для панелей с двумя плоскими или слабопрофилированными обшивками вычисляют по формуле



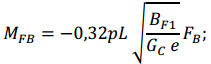




 (34)
(34)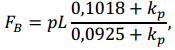 (36)
(36)