Действующий
8.4.6 Устойчивость балок сечениями 2-го и 3-го классов следует считать обеспеченной при выполнении требований перечисления а) или б) 8.4.4 при условии умножения значений  , определяемых по формулам таблицы 11, на коэффициент
, определяемых по формулам таблицы 11, на коэффициент
Учёт пластических деформаций осуществляется при расчёте балок со сжатым поясом, менее развитым, чем растянутый, - только при выполнении требований перечисления а) 8.4.4.
8.5.1 Устойчивость стенок балок 1-го класса следует считать обеспеченной, если выполнены требования 8.2.1, 8.3.1 - 8.3.3, 8.4.1 - 8.4.5 и условная гибкость стенки  (рисунок 5) не превышает значений
(рисунок 5) не превышает значений  :
:
8.5.2 Проверку устойчивости стенок балок 1-го класса следует выполнять с учётом наибольшего сжимающего напряжения 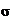 у расчетной границы стенки, принимаемого со знаком "плюс", среднего касательного напряжения
у расчетной границы стенки, принимаемого со знаком "плюс", среднего касательного напряжения  и местного напряжения
и местного напряжения  в стенке под сосредоточенной нагрузкой.
в стенке под сосредоточенной нагрузкой.
где М и Q - средние значения изгибающего момента и поперечной силы соответственно в пределах отсека; если длина отсека а (расстояние между осями поперечных ребер жесткости) больше его расчетной высоты  , то значения М и Q следует вычислять как средние для более напряжённого участка с длиной, равной
, то значения М и Q следует вычислять как средние для более напряжённого участка с длиной, равной 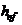 ; если в пределах отсека момент или поперечная сила меняют знак, то их средние значения следует вычислять на участке отсека с одним знаком;
; если в пределах отсека момент или поперечная сила меняют знак, то их средние значения следует вычислять на участке отсека с одним знаком;
В отсеках балки, где сосредоточенная нагрузка приложена к растянутому поясу, одновременно должны быть учтены только  и
и  или
или  и
и 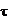 .
.
8.5.3 Устойчивость стенок балок 1-го класса симметричного сечения, укрепленных только поперечными ребрами жёсткости (рисунок 8), при наличии местного напряжения  и при условной гибкости стенки
и при условной гибкости стенки  следует считать обеспеченной, если выполнено условие
следует считать обеспеченной, если выполнено условие
8.5.4 Для балок по 8.5.3 при  коэффициент
коэффициент  в формуле (81) следует определять по таблице 12 в зависимости от вида поясных соединений и значения коэффициента
в формуле (81) следует определять по таблице 12 в зависимости от вида поясных соединений и значения коэффициента  , вычисляемого по формуле
, вычисляемого по формуле

