Действующий
Условная гибкость | Значение | |||||||
7,0 | 8,0 | 9,0 | 10 | 12 | 14 | 17 | 20 | |
0,5 | 210 | 183 | 164 | 150 | 125 | 106 | 090 | 077 |
1,0 | 196 | 175 | 157 | 142 | 121 | 103 | 086 | 074 |
1,5 | 182 | 163 | 148 | 134 | 114 | 099 | 082 | 070 |
2,0 | 170 | 153 | 138 | 125 | 107 | 094 | 079 | 067 |
2,5 | 158 | 144 | 130 | 118 | 101 | 090 | 076 | 065 |
3,0 | 147 | 135 | 123 | 112 | 097 | 086 | 073 | 063 |
3,5 | 137 | 125 | 115 | 106 | 092 | 082 | 069 | 060 |
4,0 | 127 | 118 | 108 | 098 | 088 | 078 | 066 | 057 |
4,5 | 118 | 110 | 101 | 093 | 083 | 075 | 064 | 055 |
5,0 | 111 | 103 | 095 | 088 | 079 | 072 | 062 | 053 |
5,5 | 104 | 095 | 089 | 084 | 075 | 069 | 060 | 051 |
| Примечания1 Значения коэффициентов | ||||||||
Таблица Д.4 - Коэффициенты устойчивости  при внецентренном сжатии сквозных стержней в плоскости действия момента, совпадающей с плоскостью симметрии
при внецентренном сжатии сквозных стержней в плоскости действия момента, совпадающей с плоскостью симметрии
Условная приведенная гибкость | Значение | ||||||||
0,1 | 0,25 | 0,5 | 0,75 | 1,0 | 1,25 | 1,5 | 1,75 | 2,0 | |
0,5 | 908 | 800 | 666 | 571 | 500 | 444 | 400 | 364 | 333 |
1,0 | 872 | 762 | 640 | 553 | 483 | 431 | 387 | 351 | 328 |
1,5 | 830 | 727 | 600 | 517 | 454 | 407 | 367 | 336 | 311 |
2,0 | 774 | 673 | 556 | 479 | 423 | 381 | 346 | 318 | 293 |
2,5 | 708 | 608 | 507 | 439 | 391 | 354 | 322 | 297 | 274 |
3,0 | 637 | 545 | 455 | 399 | 356 | 324 | 296 | 275 | 255 |
3,5 | 562 | 480 | 402 | 355 | 320 | 294 | 270 | 251 | 235 |
4,0 | 484 | 422 | 357 | 317 | 288 | 264 | 246 | 228 | 215 |
4,5 | 415 | 365 | 315 | 281 | 258 | 237 | 223 | 207 | 196 |
5,0 | 350 | 315 | 277 | 250 | 230 | 212 | 201 | 186 | 178 |
5,5 | 300 | 273 | 245 | 223 | 203 | 192 | 182 | 172 | 163 |
6,0 | 255 | 237 | 216 | 198 | 183 | 174 | 165 | 156 | 149 |
6,5 | 221 | 208 | 190 | 178 | 165 | 157 | 149 | 142 | 137 |
7,0 | 192 | 184 | 168 | 160 | 150 | 141 | 135 | 130 | 125 |
8,0 | 148 | 142 | 136 | 130 | 123 | 118 | 113 | 108 | 105 |
Условная приведенная гибкость | Значение | ||||||||
2.5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 | 6,5 | |
0,5 | 286 | 250 | 222 | 200 | 182 | 167 | 154 | 143 | 133 |
1,0 | 280 | 243 | 218 | 197 | 180 | 165 | 151 | 142 | 131 |
1,5 | 271 | 240 | 211 | 190 | 178 | 163 | 149 | 137 | 128 |
2,0 | 255 | 228 | 202 | 183 | 170 | 156 | 143 | 132 | 125 |
2,5 | 238 | 215 | 192 | 175 | 162 | 148 | 136 | 127 | 120 |
3,0 | 222 | 201 | 182 | 165 | 153 | 138 | 130 | 121 | 116 |
3,5 | 206 | 187 | 170 | 155 | 143 | 130 | 123 | 115 | 110 |
4,0 | 191 | 173 | 160 | 145 | 133 | 124 | 118 | 110 | 105 |
4,5 | 176 | 160 | 149 | 136 | 124 | 116 | 110 | 105 | 096 |
5.0 | 161 | 149 | 138 | 127 | 117 | 108 | 104 | 100 | 095 |
Условная приведенная гибкость | Значение | |||||||
7,0 | 8,0 | 9,0 | 10 | 12 | 14 | 17 | 20 | |
0,5 | 125 | 111 | 100 | 091 | 077 | 067 | 058 | 048 |
1,0 | 121 | 109 | 098 | 090 | 077 | 066 | 055 | 046 |
1,5 | 119 | 108 | 096 | 088 | 077 | 065 | 053 | 045 |
2,0 | 117 | 106 | 095 | 086 | 076 | 064 | 052 | 045 |
2,5 | 113 | 103 | 093 | 083 | 074 | 062 | 051 | 044 |
3,0 | 110 | 100 | 091 | 081 | 071 | 061 | 051 | 043 |
3,5 | 106 | 096 | 088 | 078 | 069 | 059 | 050 | 042 |
4,0 | 100 | 093 | 084 | 076 | 067 | 057 | 049 | 041 |
4,5 | 096 | 089 | 079 | 073 | 065 | 055 | 048 | 040 |
| Примечания1 Значения коэффициентов | ||||||||
Таблица Д.5 - Приведенные относительные эксцентриситеты  для внецентренно сжатых стержней с шарнирно опёртыми концами
для внецентренно сжатых стержней с шарнирно опёртыми концами
Эпюры моментов | Значение | |||||||||||||||
0,1 | 0,5 | 1,0 | 1,5 | 2,0 | 3,0 | 4,0 | 5,0 | 7,0 | 10,0 | 20,0 | ||||||
| 1 | 0,10 | 0,30 | 0,68 | 1,12 | 1,60 | 2,62 | 3,55 | 4,55 | 6,50 | 9,40 | 19,40 | ||||
2 | 0,10 | 0,17 | 0,39 | 0,68 | 1,03 | 1,80 | 2,75 | 3,72 | 5,65 | 8,60 | 18,50 | |||||
3 | 0,10 | 0,10 | 0,22 | 0,36 | 0,55 | 1,17 | 1,95 | 2,77 | 4,60 | 7,40 | 17,20 | |||||
4 | 0,10 | 0,10 | 0,10 | 0,18 | 0,30 | 0,57 | 1,03 | 1,78 | 3,35 | 5,90 | 15,40 | |||||
5 | 0,10 | 0,10 | 0,10 | 0,10 | 0,15 | 0,23 | 0,48 | 0,95 | 2,18 | 4,40 | 13,40 | |||||
6 | 0,10 | 0,10 | 0,10 | 0,10 | 0,10 | 0,15 | 0,18 | 0,40 | 1,25 | 3,00 | 11,40 | |||||
7 | 0,10 | 0,10 | 0,10 | 0,10 | 0,10 | 0,10 | 0,10 | 0,10 | 0,50 | 1,70 | 9,50 | |||||
| 1 | 0,10 | 0,31 | 0,68 | 1,12 | 1,60 | 2,62 | 3,55 | 4,55 | 6,50 | 9,40 | 19,40 | ||||
2 | 0,10 | 0,22 | 0,46 | 0,73 | 1,05 | 1,88 | 2,75 | 3,72 | 5,65 | 8,60 | 18,50 | |||||
3 | 0,10 | 0,17 | 0,38 | 0,58 | 0,80 | 1,33 | 2,00 | 2,77 | 4,60 | 7,40 | 17,20 | |||||
4 | 0,10 | 0,14 | 0,32 | 0,49 | 0,66 | 1,05 | 1,52 | 2,22 | 3,50 | 5,90 | 15,40 | |||||
5 | 0,10 | 0,10 | 0,26 | 0,41 | 0,57 | 0,95 | 1,38 | 1,80 | 2,95 | 4,70 | 13,40 | |||||
6 | 0,10 | 0,16 | 0,28 | 0,40 | 0,52 | 0,95 | 1,25 | 1,60 | 2,50 | 4,00 | 11,50 | |||||
7 | 0,10 | 0,22 | 0,32 | 0,42 | 0,55 | 0,95 | 1,10 | 1,35 | 2,20 | 3,50 | 10,80 | |||||
| 1 | 0,10 | 0,32 | 0,70 | 1,12 | 1,60 | 2,62 | 2,55 | 4,55 | 6,50 | 9,40 | 19,40 | ||||
2 | 0,10 | 0,28 | 0,60 | 0,90 | 1,28 | 1,96 | 2,75 | 3,72 | 5,65 | 8,40 | 18,50 | |||||
3 | 0,10 | 0,27 | 0,55 | 0,84 | 1,15 | 1,75 | 2,43 | 3,17 | 4,80 | 7,40 | 17,20 | |||||
4 | 0,10 | 0,26 | 0,52 | 0,78 | 1,10 | 1,60 | 2,20 | 2,83 | 4,00 | 6,30 | 15,40 | |||||
5 | 0,10 | 0,25 | 0,52 | 0,78 | 1,10 | 1,55 | 2,10 | 2,78 | 3,85 | 5,90 | 14,50 | |||||
6 | 0,10 | 0,28 | 0,52 | 0,78 | 1,10 | 1,55 | 2,00 | 2,70 | 3,80 | 5,60 | 13,80 | |||||
7 | 0,10 | 0,32 | 0,52 | 0,78 | 1,10 | 1,55 | 1,90 | 2,60 | 3,75 | 5,50 | 13,00 | |||||
| 1 | 0,10 | 0,40 | 0,80 | 1,23 | 1,68 | 2,62 | 3,55 | 4,55 | 6,50 | 9,10 | 19,40 | ||||
2 | 0,10 | 0,40 | 0,78 | 1,20 | 1,60 | 2,30 | 3,15 | 4,10 | 5,85 | 8,60 | 18,50 | |||||
3 | 0,10 | 0,40 | 0,77 | 1,17 | 1,55 | 2,30 | 3,10 | 3,90 | 5,55 | 8,13 | 18,00 | |||||
4 | 0,10 | 0,40 | 0,75 | 1,13 | 1,55 | 2,30 | 3,05 | 3,80 | 5,30 | 7,60 | 17,50 | |||||
5 | 0,10 | 0,40 | 0,75 | 1,10 | 1,55 | 2,30 | 3,00 | 3,80 | 5,30 | 7,60 | 17,00 | |||||
6 | 0,10 | 0,40 | 0,75 | 1,10 | 1,50 | 2,30 | 3,00 | 3,80 | 5,30 | 7,60 | 16,50 | |||||
7 | 0,10 | 0,40 | 0,75 | 1,10 | 1,40 | 2,30 | 3,00 | 3,80 | 5,30 | 7,60 | 16,00 | |||||
| Обозначения, принятые в таблице Д.5: | ||||||||||||||||
1 Коэффициент  для сечений типов 1, 2, 3, приведенных на рисунках в таблице Д.6, следует вычислять по формуле
для сечений типов 1, 2, 3, приведенных на рисунках в таблице Д.6, следует вычислять по формуле
2 Коэффициент  при расчёте на устойчивость стержня П-образного сечения на центральное сжатие (тип 4 при обозначениях, принятых в таблице Д.6, и
при расчёте на устойчивость стержня П-образного сечения на центральное сжатие (тип 4 при обозначениях, принятых в таблице Д.6, и  ) следует вычислять по формуле (Д. 1) при
) следует вычислять по формуле (Д. 1) при  и
и  (тогда В = 1), учитывая при этом, что
(тогда В = 1), учитывая при этом, что
3 Коэффициент  при расчёте на устойчивость стержня швеллерного сечения (тип 5 при обозначениях, принятых в таблице Д.6, и
при расчёте на устойчивость стержня швеллерного сечения (тип 5 при обозначениях, принятых в таблице Д.6, и  ), следует вычислять по формуле (Д.3)
), следует вычислять по формуле (Д.3)
Сечение | ||||||||
тип | схема | |||||||
1 |
| 0,25 | 0 | 0 | ||||
2 |
| По формуле (Ж.12) приложения Ж | ||||||
3 |
| 0 | То же | |||||
4 |
| 0 | ||||||
5 |
|  | 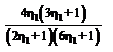 | 0 | ||||
| Обозначения, принятые в таблице Д.6: | ||||||||
4 Расчет на устойчивость внецентренно сжатых элементов двутаврового сечения с двумя осями симметрии, непрерывно подкрепленных вдоль одной из полок (рисунок Д.1), следует выполнять по формуле (111), в которой коэффициент  следует вычислять по формуле
следует вычислять по формуле
При определении  значение
значение  следует принимать равным расстоянию между сечениями элемента, закрепленными от поворота относительно продольной оси (расстояние между узлами крепления связей, распорок и т.п.).
следует принимать равным расстоянию между сечениями элемента, закрепленными от поворота относительно продольной оси (расстояние между узлами крепления связей, распорок и т.п.).
Эксцентриситет  в формуле (Д.4) считается положительным, если точка приложения силы смещена в сторону свободной полки; для центрально сжатых элементов
в формуле (Д.4) считается положительным, если точка приложения силы смещена в сторону свободной полки; для центрально сжатых элементов  .
.














