Действующий
г) для элементов с податливым шарнирным опиранием, допускающим ограниченное смещение опоры на одном конце, а на другом конце:
при внецентренном растяжении и продольной силе, приложенной между усилиями в арматуре S и  (рисунок 7.5, а):
(рисунок 7.5, а):
при продольной силе, приложенной за пределами расстояния между усилиями в арматуре S и  (рисунок 7.5, б):
(рисунок 7.5, б):
Расстояние от растягивающей продольной силы до равнодействующей усилий в арматуре определяют по формуле (7.15) без коэффициента  , т.к. нет дополнительного продольного изгиба от растягивающей силы, и без
, т.к. нет дополнительного продольного изгиба от растягивающей силы, и без  .
.
7.19 При расчете прочности в условиях воздействия температуры усилия и деформации в сечении, нормальном к продольной оси элемента, определяют на основе деформационной модели, используя уравнения равновесия внешних сил и внутренних усилий в сечении элемента с учетом изменения свойств бетона и арматуры от воздействия температуры.
Бетон по высоте сечения разбивают на элементарные участки с одинаково деформируемыми стержнями арматуры. Диаграмму деформирования бетона на сжатие строят для средней температуры бетона сжатой зоны (рисунок 5.1). Диаграмму деформирования арматуры строят для температуры ее нагрева (рисунок 5.2). До момента разрушения соблюдается условие равновесия внешних сил и внутренних усилий с учетом плоского деформирования сечения. Моментную ось удобно выбирать на сжатой грани сечения.
Критерием исчерпания прочности нормального сечения является достижение краевой деформацией сжатого бетона ее предельного значения  .
.
В сжатых колоннах при четырехстороннем воздействии температуры определяют распределение температур по сечению колонны. Сечение разбивают на полые прямоугольники с одинаковой температурой нагрева, для которых принимают равномерное распределение напряжений. Строят диаграммы деформирования бетона для температуры нагрева середины толщины каждого участка бетона и диаграммы деформирования арматуры для температуры ее нагрева.
За предельное значение деформаций укорочения с однозначной эпюрой напряжений и деформаций принимают предельную деформацию наименее нагретого бетона в сечении при однородном напряженном состоянии  при нулевой кривизне в сечении.
при нулевой кривизне в сечении.
По диаграмме деформирования для каждого участка определяют напряжения в бетоне и в арматуре, соответствующие предельной деформации бетона наименее нагретого участка.
7.20 Расчет по прочности железобетонных элементов при действии поперечных сил производят на основе модели наклонных сечений. При расчете по модели наклонных сечений должны быть обеспечены прочность элемента по полосе между наклонными сечениями и прочность по наклонному сечению на действие поперечных сил, а также прочность по наклонному сечению на действие момента.
Прочность по наклонной полосе характеризуется максимальным значением поперечной силы, которое может быть воспринято наклонной полосой, находящейся под воздействием сжимающих усилий вдоль полосы и растягивающих усилий от поперечной арматуры, пересекающей наклонную полосу. При этом прочность бетона определяют по сопротивлению бетона осевому сжатию с учетом влияния сложного напряженного состояния в наклонной полосе и средней температуре нагрева бетона наклонной полосы.
7.21 Расчет по наклонному сечению на действие поперечных сил производят на основе уравнения равновесия внешних и внутренних поперечных сил, действующих в наклонном сечении, с длиной проекции "с" на продольную ось элемента. Внутренние поперечные силы включают поперечную силу, воспринимаемую бетоном в наклонном сечении, и поперечную силу, воспринимаемую пересекающей наклонное сечение поперечной арматуры. При этом поперечные силы воспринимаемые бетоном и поперечной арматурой, определяют по сопротивлениям бетона и поперечной арматуры растяжению с учетом длины проекции "с" наклонного сечения и максимальной температуры нагрева поперечной арматуры и бетона.
7.22 Расчет по наклонному сечению на действие момента производят на основе уравнения равновесия моментов от внешних и внутренних сил, действующих в наклонном сечении, с длиной проекции "с" на продольную ось элемента. Моменты от внутренних сил включают момент, воспринимаемый пересекающей наклонное сечение продольной растянутой арматурой, и момент, воспринимаемый пересекающей наклонное сечение поперечной арматурой. При этом моменты, воспринимаемые продольной и поперечной арматурой, определяют по сопротивлениям продольной и поперечной арматуры растяжению, с учетом длины проекции "с" наклонного сечения и температуры нагрева продольной арматуры и максимальной температуры нагрева поперечной арматуры.
7.23 Расчет изгибаемых железобетонных элементов по бетонной полосе между наклонными сечениями производят из условия
7.24 Расчет изгибаемых элементов по прочности в наклонном сечении (рисунок 7.4) производят из условия

 ; (7.28)
; (7.28)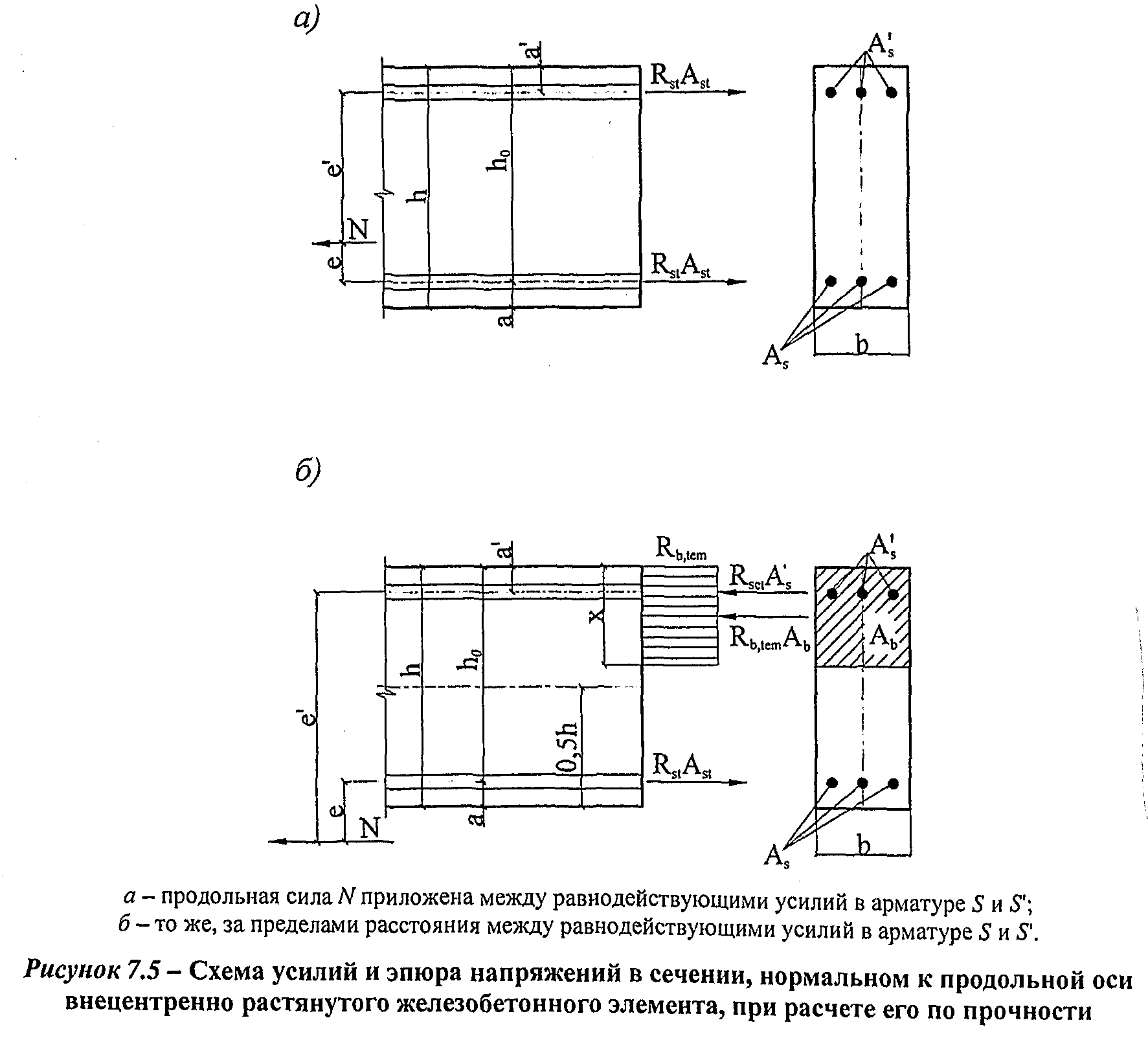
 , (7.31)
, (7.31)