Действующий
3.1. Первый метод расчета характеристик погрешности СИ в реальных условиях эксплуатации (примеры расчета см. в приложении 2).
3.1.1. Математическое ожидание М [ ] статической составляющей погрешности СИ при реальных значениях влияющих величин вычисляется по формулам:
] статической составляющей погрешности СИ при реальных значениях влияющих величин вычисляется по формулам:
Суммирование выполняется для n влияющих величин, для которых нормированы метрологические характеристики  , j = 1, 2 ... n СИ по п. 2.2.1 и значения которых в момент измерения отличаются от установленных для данного СИ нормальных значений.
, j = 1, 2 ... n СИ по п. 2.2.1 и значения которых в момент измерения отличаются от установленных для данного СИ нормальных значений.
3.1.2.1. Для вычисления  нелинейной функции влияния
нелинейной функции влияния  необходимы данные о законе распределения
необходимы данные о законе распределения  влияющей величины
влияющей величины  .
.
1. Если для СИ нормирован предел  допускаемых значений систематической составляющей основной погрешности без указания значения
допускаемых значений систематической составляющей основной погрешности без указания значения  и если нет оснований предполагать несимметричность распределения указанной погрешности в пределах
и если нет оснований предполагать несимметричность распределения указанной погрешности в пределах  , то допускается для расчетов характеристик погрешности СИ пользоваться предположением
, то допускается для расчетов характеристик погрешности СИ пользоваться предположением  .
.
2. Для СИ с индивидуальными метрологическими характеристиками (п. 2.2.1, примечание 1) для расчетов характеристик погрешности СИ принимается  .
.
3. Если для j-й влияющей величины известны только ее наименьшее  и наибольшее
и наибольшее  значения, соответствующие реальным условиям эксплуатации СИ, и нет основания выделить области предпочтительных значений влияющей величины в границах от
значения, соответствующие реальным условиям эксплуатации СИ, и нет основания выделить области предпочтительных значений влияющей величины в границах от  до
до  , несимметрично расположенные относительно центра интервала, определяемого указанными границами, то допускается для расчетов характеристик погрешности СИ пользоваться предположением
, несимметрично расположенные относительно центра интервала, определяемого указанными границами, то допускается для расчетов характеристик погрешности СИ пользоваться предположением
3.1.2. Дисперсия  статической составляющей погрешности СИ при реальных значениях влияющих величин вычисляется по формулам:
статической составляющей погрешности СИ при реальных значениях влияющих величин вычисляется по формулам:
Суммирование выполняется для n, l и k влияющих величин, для которых нормированы метрологические характеристики  , j = 1, 2 ... n;
, j = 1, 2 ... n;  , j = 1, 2 ... l;
, j = 1, 2 ... l;  , j = 1, 2 ... k по п. 2.2.1 и значения которых в момент измерения отличаются от установленных для данного СИ нормальных значений.
, j = 1, 2 ... k по п. 2.2.1 и значения которых в момент измерения отличаются от установленных для данного СИ нормальных значений.
3.1.2.2. Для вычисления  нелинейной функции влияния
нелинейной функции влияния  необходимы данные о законе распределения
необходимы данные о законе распределения  влияющей величины
влияющей величины 
1. Если для СИ нормирован предел  допускаемых значений систематической составляющей основной погрешности без указания значения
допускаемых значений систематической составляющей основной погрешности без указания значения  и если нет оснований предполагать несимметричность и полимодальность распределения указанной погрешности в пределах
и если нет оснований предполагать несимметричность и полимодальность распределения указанной погрешности в пределах  , то допускается для расчетов характеристик погрешности СИ пользоваться предположением
, то допускается для расчетов характеристик погрешности СИ пользоваться предположением  .
.
2. Для СИ с индивидуальными метрологическими характеристиками (п. 2.2.1, примечание 1) для расчетов характеристик погрешности СИ принимается  .
.
3. Если для j-й влияющей величины известны только ее наименьшее  и наибольшее
и наибольшее  значения, соответствующие реальным условиям эксплуатации СИ, и нет оснований выделить области предпочтительных значений влияющей величины в границах от
значения, соответствующие реальным условиям эксплуатации СИ, и нет оснований выделить области предпочтительных значений влияющей величины в границах от  до
до  , за исключением, может быть, области вокруг центра интервала, определяемого указанными границами, то допускается для расчетов характеристик погрешности СИ пользоваться предположением
, за исключением, может быть, области вокруг центра интервала, определяемого указанными границами, то допускается для расчетов характеристик погрешности СИ пользоваться предположением
3.1.3. Дисперсия  приведенной к выходу динамической составляющей погрешности аналогового СИ вычисляется по формуле
приведенной к выходу динамической составляющей погрешности аналогового СИ вычисляется по формуле
1. Если в качестве характеристики входного сигнала задана его автокорреляционная функция  (п. 2.2.3), то предварительно вычисляется спектральная плотность входного сигнала по формуле
(п. 2.2.3), то предварительно вычисляется спектральная плотность входного сигнала по формуле
2. Если в качестве динамической характеристики нормирована передаточная функция  (п. 2.2.1), то предварительно заменой аргумента S на
(п. 2.2.1), то предварительно заменой аргумента S на  получают амплитудно-фазовую характеристику
получают амплитудно-фазовую характеристику  .
.









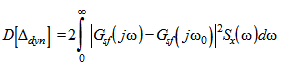
 . (12)
. (12) . (13)
. (13)