Действующий
М - сосредоточенный изгибающий момент от внешней нагрузки, учитываемый при расчете на продавливание (6.2.46);
В железобетонном каркасе зданий с плоскими перекрытиями сосредоточенный изгибающий момент  равен суммарному изгибающему моменту в сечениях верхней и нижней колонн, примыкающих к перекрытию в рассматриваемом узле.
равен суммарному изгибающему моменту в сечениях верхней и нижней колонн, примыкающих к перекрытию в рассматриваемом узле.
При действии изгибающих моментов в двух взаимно перпендикулярных плоскостях расчет производят из условия
где F,  и
и  - сосредоточенные сила и изгибающие моменты в направлениях осей X и Y, учитываемые при расчете на продавливание (6.2.46), от внешней нагрузки;
- сосредоточенные сила и изгибающие моменты в направлениях осей X и Y, учитываемые при расчете на продавливание (6.2.46), от внешней нагрузки;
Усилия  и
и  определяют согласно указаниям, приведенным выше, при действии момента соответственно в плоскости оси Х и в плоскости оси Y.
определяют согласно указаниям, приведенным выше, при действии момента соответственно в плоскости оси Х и в плоскости оси Y.
При расположении сосредоточенной силы внецентренно относительно центра тяжести контура расчетного поперечного сечения значения изгибающих сосредоточенных моментов от внешней нагрузки определяют с учетом дополнительного момента от внецентренного приложения сосредоточенной силы относительно центра тяжести контура расчетного поперечного сечения.
6.2.50 Расчет прочности элементов с поперечной арматурой на продавливание при действии сосредоточенных силы и изгибающего момента (рисунок 6.14) производят из условия
Усилие  , воспринимаемое поперечной арматурой, нормальной к плоскости элемента и расположенной равномерно вдоль контура расчетного сечения, определяют по формуле
, воспринимаемое поперечной арматурой, нормальной к плоскости элемента и расположенной равномерно вдоль контура расчетного сечения, определяют по формуле
При действии сосредоточенных изгибающих моментов в двух взаимно перпендикулярных плоскостях расчет производят из условия
Усилия  и
и  определяют согласно указаниям, приведенным выше, при действии изгибающего момента соответственно в направлении оси X и оси Y.
определяют согласно указаниям, приведенным выше, при действии изгибающего момента соответственно в направлении оси X и оси Y.
6.2.51 В общем случае значения момента сопротивления расчетного контура бетона при продавливании  в направлениях взаимно перпендикулярных осей X и Y определяют по формуле
в направлениях взаимно перпендикулярных осей X и Y определяют по формуле
где  - момент инерции расчетного контура относительно осей
- момент инерции расчетного контура относительно осей  и
и  , проходящих через его центр тяжести (рисунок 6.12);
, проходящих через его центр тяжести (рисунок 6.12);
Значение момента инерции  определяют как сумму моментов инерции
определяют как сумму моментов инерции  отдельных участков расчетного контура поперечного сечения относительно центральных осей, проходящих через центр тяжести расчетного контура.
отдельных участков расчетного контура поперечного сечения относительно центральных осей, проходящих через центр тяжести расчетного контура.
Для замкнутого прямоугольного контура (рисунок 6.12, а, г) с длиной участков  и
и  в направлении осей Х и Y центр тяжести расположен в месте пересечения осей симметрии контура.
в направлении осей Х и Y центр тяжести расположен в месте пересечения осей симметрии контура.
Значения  определяют по формулам (6.112) и (6.113), принимая условно ширину каждого участка контура длиной
определяют по формулам (6.112) и (6.113), принимая условно ширину каждого участка контура длиной  и
и  , равной единице:
, равной единице:

 , (6.105)
, (6.105)
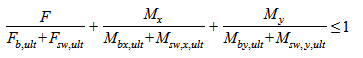
 , (6.109)
, (6.109) , (6.110)
, (6.110) ; (6.112)
; (6.112) (6.114)
(6.114)