Действующий
6.2.31 Предельные значения относительных деформаций бетона  принимают при двузначной эпюре деформаций (сжатие и растяжение) в поперечном сечении бетона элемента (изгиб, внецентренное сжатие или растяжение с большими эксцентриситетами) равными
принимают при двузначной эпюре деформаций (сжатие и растяжение) в поперечном сечении бетона элемента (изгиб, внецентренное сжатие или растяжение с большими эксцентриситетами) равными 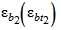 .
.
При внецентренном сжатии или растяжении элементов и распределении в поперечном сечении бетона элемента деформаций только одного знака предельные значения относительных деформаций бетона  определяют в зависимости от соотношения деформаций бетона на противоположных гранях сечения элемента
определяют в зависимости от соотношения деформаций бетона на противоположных гранях сечения элемента  и
и  по формулам:
по формулам:
6.2.32 Расчет по прочности железобетонных элементов при действии поперечных сил производят на основе модели наклонных сечений.
При расчете по модели наклонных сечений должны быть обеспечены прочность элемента по полосе между наклонными сечениями и по наклонному сечению на действие поперечных сил, а также прочность по наклонному сечению на действие момента.
Прочность по наклонной полосе характеризуется максимальным значением поперечной силы, которое может быть воспринято наклонной полосой, находящейся под воздействием сжимающих усилий вдоль полосы и растягивающих усилий от поперечной арматуры, пересекающей наклонную полосу. При этом прочность бетона определяют по сопротивлению бетона осевому сжатию с учетом влияния сложного напряженного состояния в наклонной полосе.
Расчет по наклонному сечению на действие поперечных сил производят на основе уравнения равновесия внешних и внутренних поперечных сил, действующих в наклонном сечении с длиной проекции с на продольную ось элемента. Внутренние поперечные силы включают поперечную силу, воспринимаемую бетоном в наклонном сечении, и поперечную силу, воспринимаемую пересекающей наклонное сечение поперечной арматурой. При этом поперечные силы, воспринимаемые бетоном и поперечной арматурой, определяют по сопротивлениям бетона и поперечной арматуры растяжению с учетом длины проекции с наклонного сечения.
Расчет по наклонному сечению на действие момента производят на основе уравнения равновесия моментов от внешних и внутренних сил, действующих в наклонном сечении с длиной проекции с на продольную ось элемента. Моменты от внутренних сил включают момент, воспринимаемый пересекающей наклонное сечение продольной растянутой арматурой, и момент, воспринимаемый пересекающей наклонное сечение поперечной арматурой. При этом моменты, воспринимаемые продольной и поперечной арматурой, определяют по сопротивлениям продольной и поперечной арматуры растяжению с учетом длины проекции с наклонного сечения.
6.2.33 Расчет изгибаемых железобетонных элементов по бетонной полосе между наклонными сечениями производят из условия
где Q - поперечная сила в наклонном сечении с длиной проекции с на продольную ось элемента, определяемая от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;
Расчет производят для ряда расположенных по длине элемента наклонных сечений при наиболее опасной длине проекции наклонного сечения с. При этом длину с в формуле (6.68) принимают не более  .
.
Допускается производить расчет наклонных сечений, не рассматривая наклонные сечения при определении поперечной силы от внешней нагрузки, из условия
При расположении нормального сечения, в котором учитывают поперечную силу  , вблизи опоры на расстоянии а менее
, вблизи опоры на расстоянии а менее  расчет из условия (6.70) производят, умножая значения
расчет из условия (6.70) производят, умножая значения  , определяемые по формуле (6.71), на коэффициент, равный
, определяемые по формуле (6.71), на коэффициент, равный  , но принимают значение
, но принимают значение  не более
не более  .
.
При расположении нормального сечения, в котором учитывают поперечную силу  , на расстоянии а менее
, на расстоянии а менее  расчет из условия (6.70) производят, умножая значение
расчет из условия (6.70) производят, умножая значение  , определяемое по формуле (6.72), на коэффициент, равный
, определяемое по формуле (6.72), на коэффициент, равный 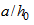 .
.
Можно учитывать поперечную арматуру и при невыполнении этого условия, если в условии (6.66) принимать

 ; (6.63)
; (6.63)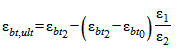 ; (6.64)
; (6.64) , (6.67)
, (6.67) . (6.69)
. (6.69)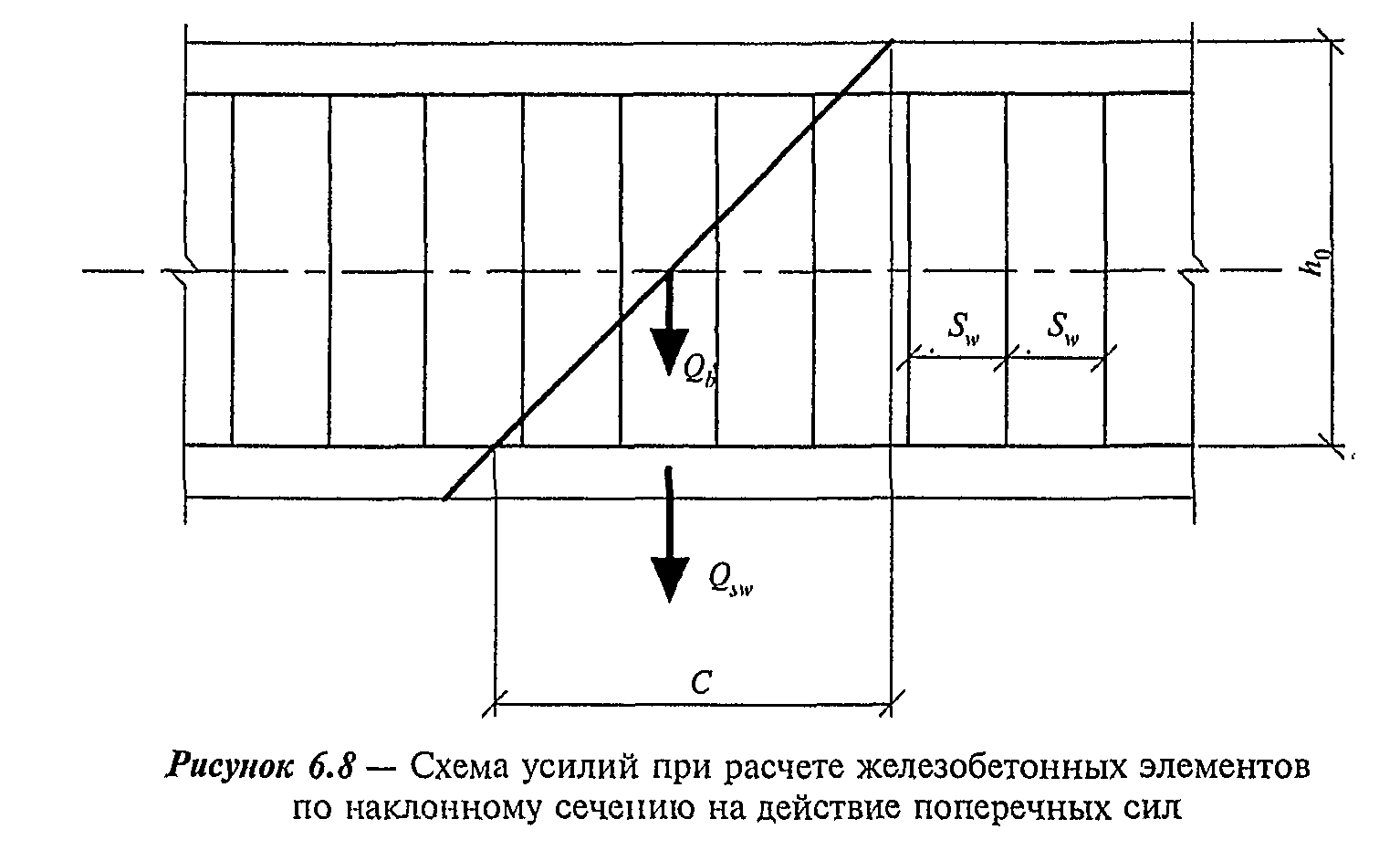
 .
.