Действующий
Транспонирование, перемножение и обращение матриц осуществляют по стандартным процедурам, имеющимся в библиотеках подпрограмм ЭВМ.
с начальными условиями  . В уравнении (76) символ f использован для обозначения правой части уравнения (65).
. В уравнении (76) символ f использован для обозначения правой части уравнения (65).
 . В уравнении (76) символ f использован для обозначения правой части уравнения (65).
. В уравнении (76) символ f использован для обозначения правой части уравнения (65).В процессе вычислений для нахождения доверительных интервалов (см. формулу (81) найденных параметров получают информационную матрицу Фишера
1.3.3.2. По методу Давидона-Флетчера-Пауэла итерационный процесс минимизации функционала (72) проводят по формуле (73), в которой  определяют по формуле
определяют по формуле
стремится в конце итерационного процесса к обратной матрице частных производных второго порядка  в точке минимума;
в точке минимума;
 в точке минимума;
в точке минимума;

|
|
| 146 × 115 пикс. Открыть в новом окне | |

|
|
| 320 × 65 пикс. Открыть в новом окне | |
 находится аналогично элементам матрицы
находится аналогично элементам матрицы Прекращение итерационного процесса происходит при выполнении условия  , где
, где  - заданная точность вычисления.
- заданная точность вычисления.
Целесообразно задавать  несколько больше, чем
несколько больше, чем 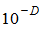 , где D - число значащих цифр в представлении с плавающей запятой в ЭВМ.
, где D - число значащих цифр в представлении с плавающей запятой в ЭВМ.
В ходе построения итерационного процесса аналогично предыдущему методу нелинейных оценок получают информационную матрицу Фишера  .
.
Для обоих изложенных выше методов доверительный интервал значений, определяемых в процессе оптимизации параметров, вычисляют при заданной доверительной вероятности в соответствии с условием

 - матрица размерностью 2хN;
- матрица размерностью 2хN;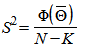 , (78)
, (78)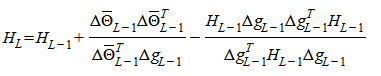

 - вектор-столбец неизвестных параметров;
- вектор-столбец неизвестных параметров; , (83)
, (83)