Действующий
Сравнение экспериментальной и расчетной зависимостей изменения радиуса пламени от времени может быть использовано для контроля правильности определения нормальной скорости.
В приближении адиабатического сжатия смеси изменение нормальной скорости с ростом относительного давления описывается выражением
Входящие в расчетные формулы параметры  ,
,  ,
,  определяют термодинамическим расчетом. При отсутствии расчетных значений
определяют термодинамическим расчетом. При отсутствии расчетных значений  и
и  вычисления могут проводиться в приближении
вычисления могут проводиться в приближении  а значение
а значение  может быть заимствовано из экспериментальных данных.
может быть заимствовано из экспериментальных данных.
1.3.2. Из экспериментальной записи изменения давления во времени выбирают не менее пяти значений  (
( ), удовлетворяющих условию
), удовлетворяющих условию
Примечание. Для оценки соответствия энергии искры условиям испытания используют экспериментальную точку  , соответствующую моменту срабатывания зажигающего устройства. При этом считают, что энергия искры соответствует условиям испытания, если расчетная зависимость изменения давления, полученная в результате оптимизации, совпадает с экспериментальной, включая точку
, соответствующую моменту срабатывания зажигающего устройства. При этом считают, что энергия искры соответствует условиям испытания, если расчетная зависимость изменения давления, полученная в результате оптимизации, совпадает с экспериментальной, включая точку  .
.
1.3.3. Оптимизируют расчетную зависимость изменения давления внутри сосуда по экспериментальной путем минимизации функционала 
Транспонирование, перемножение и обращение матриц осуществляют по стандартным процедурам, имеющимся в библиотеках подпрограмм ЭВМ.
с начальными условиями  . В уравнении (76) символ f использован для обозначения правой части уравнения (65).
. В уравнении (76) символ f использован для обозначения правой части уравнения (65).
 . В уравнении (76) символ f использован для обозначения правой части уравнения (65).
. В уравнении (76) символ f использован для обозначения правой части уравнения (65).В процессе вычислений для нахождения доверительных интервалов (см. формулу (81) найденных параметров получают информационную матрицу Фишера
1.3.3.2. По методу Давидона-Флетчера-Пауэла итерационный процесс минимизации функционала (72) проводят по формуле (73), в которой  определяют по формуле
определяют по формуле

 - термокинетичeский показатель.
- термокинетичeский показатель.
 - вектор-столбец неизвестных параметров;
- вектор-столбец неизвестных параметров; - матрица размерностью 2хN;
- матрица размерностью 2хN;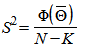 , (78)
, (78)